Distribution normale

 Les données peuvent être "distribuées" (étalées) de différentes manières.

Il peut être étalé plus à gauche		Ou plus à droite

Ou tout peut être mélangé

Mais il existe de nombreux cas où les données ont tendance à se situer autour d'une valeur centrale sans biais à gauche ou à droite, et elles se rapprochent d'une « distribution normale » comme celle-ci :

Une distribution normale

La "courbe en cloche" est une distribution normale.
Et le jaunehistogrammemontre quelques données qui le
suivent de près, mais pas parfaitement (ce qui est habituel).

On l'appelle souvent une "courbe en cloche" parce qu'elle ressemble à une cloche.

Beaucoup de choses suivent de près une distribution normale :

• hauteurs de personnes
• taille des choses produites par des machines
• erreurs dans les mesures
• pression artérielle
• notes sur un test

Nous disons que les données sont "normalement distribuées":

La  distribution normale  a :

• moyenne = médiane = mode
• symétrie autour du centre
• 50 % des valeurs inférieures à la moyenne
  et 50 % supérieures à la moyenne

Quincunx

Vous pouvez voir une distribution normale créée par hasard ! Il s'appelle le Quincunx et c'est une machine incroyable. Amusez-vous avec !

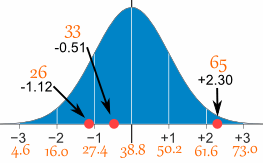
Ecarts types

Les Écart-type est une mesure de l'étalement des nombres (lisez cette page pour plus de détails sur la façon de le calculer).

quand nous calculer l'écart typeon trouve que généralement :

68 % des valeurs sont à moins de 1 écart type de la moyenne     95% des valeurs sont dans les 2 écarts types de la moyenne     99,7 % des valeurs sont à moins de 3 écarts-types de la moyenne

 

Exemple : 95% des élèves de l'école mesurent entre 1,1m et 1,7m .

En supposant que ces données soient normalement distribuées, pouvez-vous calculer la moyenne et l'écart type ?

La moyenne est à mi-chemin entre 1,1m et 1,7m :

Moyenne = (1,1m + 1,7m) / 2 = 1,4m

95% correspond à 2 écarts types de chaque côté de la moyenne (un total de 4 écarts types) donc :

1 écart type	= (1,7m-1,1m) / 4
	= 0,6m / 4
	= 0,15m

Et voici le résultat :

Il est bon de connaître l'écart type, car on peut dire que toute valeur est :

• susceptible d'être inférieur à 1 écart type (68 sur 100 devraient être)
• très probablement dans les 2 écarts types (95 sur 100 devraient être)
• presque certainement dans les 3 écarts types (997 sur 1000 devraient être)

Notes standard

Le nombre d' écarts types par rapport à la moyenne est également appelé « score standard », « sigma » ou « z-score ». Habituez-vous à ces mots !

Exemple : Dans cette même école, un de vos amis mesure 1,85 m

 

Vous pouvez voir sur la courbe en cloche que 1,85m correspond à 3 écarts types par rapport à la moyenne de 1,4, donc :

La taille de votre ami a un "z-score" de 3,0

Il est également possible de calculer combien d'écarts types 1,85 est de la moyenne

À quelle distance est 1,85 de la moyenne ?

Il est à 1,85 - 1,4 = 0,45m de la moyenne

Cela fait combien d'écarts types ? L'écart type est de 0,15m, donc :

0,45m / 0,15m = 3 écarts types

Donc, pour convertir une valeur en un score standard ("z-score") :

• soustraire d'abord la moyenne,
• puis diviser par l'écart type

Et cela s'appelle « Standardiser » :

Nous pouvons prendre n'importe quelle distribution normale et la convertir en distribution normale standard.

Exemple : temps de trajet

Une enquête sur le temps de trajet quotidien a donné ces résultats (en minutes) :

26, 33, 65, 28, 34, 55, 25, 44, 50, 36, 26, 37, 43, 62, 35, 38, 45, 32, 28, 34

La moyenne est de 38,8 minutes et l' écart type est de 11,4 minutes (vous pouvez copier et coller les valeurs dans leCalculateur d'écart type si tu veux).

Convertissez les valeurs en scores z (« scores standard »).

 

Pour convertir 26 :

soustraire d'abord la moyenne : 26 − 38,8 = −12,8,

puis diviser par l'écart type : −12,8/11,4 = −1,12

Donc 26 est -1,12 Ecarts-types par rapport à la moyenne

 

Voici les trois premières conversions

Valeur d'origine	Calcul	Score standard (z-score)
26	(26-38,8) / 11,4 =	-1,12
33	(33-38,8) / 11,4 =	−0,51
65	(65-38,8) / 11,4 =	+2,30
...	...	...

 

Et les voici graphiquement :

Vous pouvez calculer vous-même le reste des scores z !

 

La formule du score z que nous avons utilisée est :

z = x − μ??

• z est le "z-score" (score standard)
• x est la valeur à normaliser
• μ ( «mu») est la moyenne
• σ ("sigma") est l'écart type

Et voici comment l'utiliser :

Exemple : Temps de trajet (suite)

Voici les trois premières conversions utilisant la "formule du score z" :

z = x − μ??

• = 38,8
• = 11,4

X	x − μ??	z (z-score)
26	26 − 38,811,4	= -1,12
33	33 − 38,811,4	= −0,51
65	65 − 38,811,4	= +2,30
...	...	...

Les calculs exacts que nous avons faits avant, juste en suivant la formule.

Pourquoi standardiser... ?

Cela peut nous aider à prendre des décisions concernant nos données.

Exemple : le professeur Willoughby corrige un examen.

Voici les résultats des élèves (sur 60 points) :

20, 15, 26, 32, 18, 28, 35, 14, 26, 22, 17

La plupart des étudiants n'ont même pas obtenu 30 sur 60, et la plupart échoueront .

Le test a dû être très difficile, alors le professeur décide de standardiser tous les scores et d'échouer uniquement les personnes ayant plus d'un écart-type en dessous de la moyenne.

La moyenne est de 23 et l' écart-type est de 6,6 , et voici les scores standard :

-0,45, -1,21 , 0,45, 1,36, -0,76, 0,76, 1,82, -1,36 , 0,45, -0,15, -0,91

Désormais, seuls 2 étudiants échoueront (ceux inférieurs à −1 écart type)

Beaucoup plus juste !

Cela facilite aussi la vie car nous n'avons besoin que d'une seule table (la Tableau de distribution normale standard), plutôt que d'effectuer des calculs individuellement pour chaque valeur de moyenne et d'écart type.

Plus en détail

Voici la distribution normale standard avec des pourcentages pour chaque moitié d'un écart type et des pourcentages cumulés :

Exemple : Votre score dans un test récent était de 0,5 écart-type au-dessus de la moyenne, combien de personnes ont obtenu un score inférieur à vous ?

• Entre 0 et 0,5 c'est 19,1%
• Moins de 0 équivaut à 50 % (moitié gauche de la courbe)

Donc le total inférieur à vous est :

50% + 19,1% = 69,1%

En théorie, 69,1% ont obtenu moins que vous (mais avec des données réelles, le pourcentage peut être différent)

Un exemple pratique : votre entreprise conditionne le sucre dans des sacs de 1 kg.

Lorsque vous pesez un échantillon de sacs, vous obtenez ces résultats :

• 1007g, 1032g, 1002g, 983g, 1004g, ... (une centaine de mesures)
• Moyenne = 1010g
• Écart type = 20g

Certaines valeurs sont inférieures à 1000g... pouvez-vous corriger cela ?

La distribution normale de vos mesures ressemble à ceci :

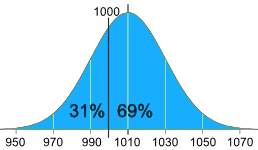
31% des sacs font moins de 1000g,
ce qui trompe le client !

C'est une chose aléatoire, donc nous ne pouvons pas arrêter les sacs de moins de 1000g, mais nous pouvons essayer de le réduire beaucoup.

Ajustons la machine pour que 1000g soit :

à -3 écarts types :
De la grande courbe en cloche ci-dessus, nous voyons que 0,1% sont moins. Mais c'est peut-être trop petit.
à −2,5 écarts-types :
En dessous de 3 c'est 0,1% et entre 3 et 2,5 écarts types c'est 0,5%, ensemble c'est 0,1% + 0,5% = 0,6% (un bon choix je pense)

Ajustons donc la machine pour avoir 1000g à -2,5 écarts types par rapport à la moyenne.

Maintenant, nous pouvons l'ajuster à:

• augmenter la quantité de sucre dans chaque sachet (ce qui change la moyenne), ou
• le rendre plus précis (ce qui réduit l'écart type)

Essayons les deux.

Ajustez la quantité moyenne dans chaque sac

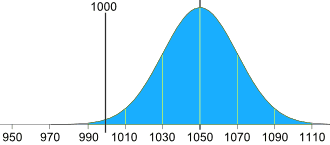
L'écart type est de 20g, et nous en avons besoin de 2,5 :

2,5 × 20g = 50g

La machine devrait donc en moyenne 1050g , comme ceci :

 

Ajuster la précision de la machine

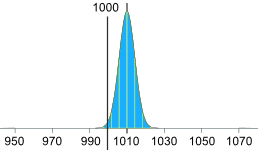
Ou nous pouvons garder la même moyenne (de 1010g), mais alors nous avons besoin de 2,5 écarts types pour être égal à 10g :

10g / 2,5 = 4g

L'écart type devrait donc être de 4g , comme ceci :

(Nous espérons que la machine est aussi précise !)

Ou peut-être pourrions-nous combiner une meilleure précision et une taille moyenne légèrement plus grande, je vous laisse le soin de décider !