Les degrés de liberté (DF) dans les statistiques indiquent le nombre de valeurs indépendantes qui peuvent varier dans une analyse sans rompre aucune contrainte. C'est une idée essentielle qui apparaît dans de nombreux contextes à travers les statistiques, y compris les tests d'hypothèses , les distributions de probabilité et l'analyse de régression . Découvrez comment ce concept fondamental affecte la puissance et la précision de votre analyse !
Dans cet article de blog, je donne vie à ce concept de manière intuitive. Je vais commencer par définir les degrés de liberté et fournir la formule. Cependant, je passerai rapidement à des exemples pratiques dans le cadre de diverses analyses statistiques car ils facilitent la compréhension de ce concept.
Définition des degrés de liberté
Que sont les degrés de liberté en statistique ? Les degrés de liberté sont le nombre de valeurs indépendantes qu'une analyse statistique peut estimer . Vous pouvez également le considérer comme le nombre de valeurs qui sont libres de varier au fur et à mesure que vous estimez les paramètres . Je sais, ça commence à paraître un peu trouble !
DF englobe la notion selon laquelle la quantité d'informations indépendantes dont vous disposez limite le nombre de paramètres que vous pouvez estimer. En règle générale, les degrés de liberté sont égaux à la taille de votre échantillon moins le nombre de paramètres que vous devez calculer au cours d'une analyse. Il s'agit généralement d'un nombre entier positif.
Les degrés de liberté sont une combinaison de la quantité de données dont vous disposez et du nombre de paramètres que vous devez estimer. Il indique la quantité d'informations indépendantes entrant dans une estimation de paramètre . Dans cette veine, il est facile de voir que vous voulez que beaucoup d'informations entrent dans les estimations de paramètres pour obtenir des estimations plus précises et des tests d'hypothèses plus puissants. Alors, vous voulez beaucoup de DF !
Informations indépendantes et contraintes sur les valeurs
Les définitions des degrés de liberté parlent d'informations indépendantes. Vous pourriez penser que cela fait référence à la taille de l'échantillon, mais c'est un peu plus compliqué que cela. Pour comprendre pourquoi, il faut parler de la liberté de varier. La meilleure façon d'illustrer ce concept est avec un exemple.
Supposons que nous collectons l' échantillon aléatoire d'observations indiqué ci-dessous. Maintenant, imaginons que nous connaissions la moyenne, mais que nous ne connaissions pas la valeur d'une observation—le X dans le tableau ci-dessous.

La moyenne est de 6,9 et elle est basée sur 10 valeurs. Ainsi, nous savons que les valeurs doivent totaliser 69 sur la base de l'équation de la moyenne.
En utilisant une algèbre simple (64 + X = 69), nous savons que X doit être égal à 5.
Article connexe : Qu'est-ce que la moyenne dans les statistiques ?
Comment trouver les degrés de liberté en statistique
Comme vous pouvez le voir, ce dernier nombre n'a aucune liberté de varier. Ce n'est pas une information indépendante car elle ne peut pas être une autre valeur. L'estimation du paramètre, la moyenne dans ce cas, impose une contrainte sur la liberté de variation. La dernière valeur et la moyenne sont entièrement dépendantes l'une de l'autre. Par conséquent, après avoir estimé la moyenne, nous n'avons que 9 informations indépendantes, même si la taille de notre échantillon est de 10.
C'est l'idée de base des degrés de liberté en statistique. Dans un sens général, DF est le nombre d'observations dans un échantillon qui sont libres de varier lors de l'estimation des paramètres statistiques. Vous pouvez également le considérer comme la quantité de données indépendantes que vous pouvez utiliser pour estimer un paramètre.
Formule des degrés de liberté
La formule pour trouver les degrés de liberté est simple. Les degrés de liberté sont égaux à la taille de l'échantillon moins le nombre de paramètres que vous estimez :
DF = N - P
Où:
- N = taille de l'échantillon
- P = le nombre de paramètres ou de relations
Par exemple, les degrés de liberté pour un test t à 1 échantillon sont égaux à N – 1 parce que vous estimez un paramètre, la moyenne.
La formule de calcul des degrés de liberté d'un tableau dans un test du chi carré est (r-1) (c-1), où r = le nombre de lignes et c = le nombre de colonnes.
DF et distributions de probabilité
Les degrés de liberté définissent également les distributions de probabilité pour les statistiques de test de divers tests d'hypothèse. Par exemple, les tests d'hypothèses utilisent la distribution t, la distribution F et la distribution du chi carré pour déterminer la signification statistique. Chacune de ces distributions de probabilité est une famille de distributions où le DF définit la forme. Les tests d'hypothèse utilisent ces distributions pour calculer les valeurs de p. Ainsi, le DF est directement lié aux p-values via ces distributions !
Voyons ensuite comment ces distributions fonctionnent pour plusieurs tests d'hypothèse.
Related posts : Comprendre les distributions de probabilité et un regard graphique sur les niveaux de signification (Alpha) et les valeurs P
Degrés de liberté pour les tests t et la distribution t
Les tests T sont des tests d'hypothèse pour la moyenne et utilisent la distribution t pour déterminer la signification statistique.
Un test t à 1 échantillon détermine si la différence entre la moyenne de l'échantillon et la valeur de l' hypothèse nulle est statistiquement significative. Revenons à notre exemple de la moyenne ci-dessus. Nous savons que lorsque vous avez un échantillon et que vous estimez la moyenne, vous avez n – 1 degrés de liberté, où n est la taille de l'échantillon. Par conséquent, pour un test t à 1 échantillon, les degrés de liberté sont égaux à n – 1.
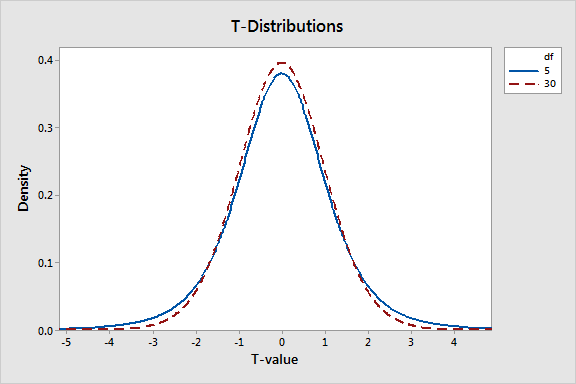
Le DF définit la forme de la distribution t que votre test t utilise pour calculer la valeur p . Le graphique ci-dessous montre la distribution t pour plusieurs degrés de liberté différents. Étant donné que les degrés de liberté sont si étroitement liés à la taille de l'échantillon, vous pouvez voir l'effet de la taille de l'échantillon. Au fur et à mesure que le DF diminue, la distribution t a des queues plus épaisses. Cette propriété tient compte de la plus grande incertitude associée aux petites tailles d'échantillon.
Le graphique des degrés de liberté ci-dessous affiche les distributions t.
Pour approfondir les tests t, lisez mon article sur le fonctionnement des tests t . Je montre comment les différents tests t calculent les valeurs t et utilisent les distributions t pour calculer les valeurs p.
Le test F de l'ANOVA teste également les moyennes des groupes. Il utilise la distribution F, qui est définie par le DF. Cependant, vous calculez les degrés de liberté ANOVA différemment car vous devez trouver le numérateur et le dénominateur DF. Pour plus d'informations, lisez mon article sur le fonctionnement des tests F dans ANOVA .
Vous trouverez souvent des degrés de liberté dans les tableaux avec leurs valeurs critiques. Les statisticiens recherchent DF dans ces tableaux pour déterminer si la statistique de test pour leur test d'hypothèse se situe dans la région critique, indiquant une signification statistique.
Article connexe : Comment interpréter correctement les valeurs P
Degrés de liberté pour les tableaux dans les tests du Khi deux
Le test d'indépendance du chi carré détermine s'il existe une relation statistiquement significative entre les variables catégorielles d'un tableau. Tout comme les autres tests d'hypothèse, ce test intègre DF. Pour un tableau avec r lignes et c colonnes, la formule pour trouver les degrés de liberté pour un test du Khi deux est (r-1) (c-1).
Cependant, nous pouvons créer des tableaux pour comprendre comment trouver leurs degrés de liberté de manière plus intuitive. Le DF pour un test d'indépendance du Khi-deux est le nombre de cellules du tableau qui peut varier avant de pouvoir calculer toutes les autres cellules. Dans un tableau chi carré, les cellules représentent la fréquence observée pour chaque combinaison de variables catégorielles. Les contraintes sont les totaux dans les marges.
Chi-Square 2 X 2 Table
Par exemple, dans un tableau 2 X 2, après avoir entré une valeur dans le tableau, vous pouvez calculer les cellules restantes.

Dans le tableau ci-dessus, j'ai entré le 15 gras, puis je peux calculer les trois valeurs restantes entre parenthèses. Par conséquent, cette table a 1 DF.
Chi-Square 3 X 2 Table
Maintenant, essayons une table 3 X 2. Le tableau ci-dessous illustre l'exemple que j'utilise dans mon article sur le test d'indépendance du chi carré. Dans cet article, je détermine s'il existe une relation statistiquement significative entre la couleur uniforme et les décès dans la série télévisée originale Star Trek .

Dans le tableau, une variable catégorielle est la couleur de la chemise, qui peut être bleue, dorée ou rouge. L'autre variable catégorielle est le statut, qui peut être mort ou vivant. Après avoir entré les deux valeurs en gras, je peux calculer toutes les cellules restantes. Par conséquent, cette table a 2 DF.
Lisez mon article, Test d'indépendance du chi carré et un exemple , pour voir comment ce test fonctionne et comment interpréter les résultats à l'aide de l' exemple Star Trek .
Comme la distribution t, la distribution du chi carré est une famille de distributions où les degrés de liberté définissent la forme. Les tests du chi carré utilisent cette distribution pour calculer les valeurs de p. Le graphique des degrés de liberté ci-dessous affiche plusieurs distributions du Khi deux.

Degrés de liberté dans l'analyse de régression
Trouver les degrés de liberté dans la régression est un peu plus compliqué, et je vais rester simple. Repensez à la formule générale pour DF, N – P. Dans un modèle de régression, chaque terme est un paramètre estimé qui utilise un degré de liberté. Dans la sortie de régression ci-dessous, vous pouvez voir comment chaque terme nécessite un DF. Il y a 28 observations et les deux variables indépendantes utilisent un total de deux DF. La sortie affiche les 26 degrés de liberté restants en erreur.

Les erreurs DF sont les informations indépendantes disponibles pour estimer vos coefficients . Pour des estimations de coefficients précises et des tests d'hypothèses puissants dans la régression, vous devez avoir de nombreux degrés de liberté d'erreur, ce qui équivaut à avoir de nombreuses observations pour chaque terme du modèle.
Au fur et à mesure que vous ajoutez des termes au modèle, les degrés de liberté d'erreur diminuent. Vous disposez de moins d'informations pour estimer les coefficients. Cette situation réduit la précision des estimations et la puissance des tests. Lorsque vous avez trop peu de DF restants, vous ne pouvez pas faire confiance aux résultats de la régression. Si vous utilisez tous vos degrés de liberté, la procédure ne peut pas calculer les valeurs p.
Pour plus d'informations sur les problèmes qui surviennent lorsque vous utilisez trop de DF et sur le nombre d'observations dont vous avez besoin, lisez mon article de blog sur le surajustement de votre modèle .
Même s'ils peuvent paraître obscurs, les degrés de liberté sont essentiels à toute analyse statistique ! En un mot, DF définit la quantité d'informations dont vous disposez par rapport au nombre de propriétés que vous souhaitez estimer. Si vous n'avez pas assez de données pour ce que vous voulez faire, vous aurez des estimations imprécises et une faible puissance statistique .


