Cette section couvre les permutations et les combinaisons.
Disposition des objets
Le nombre de façons d'organiser n objets différents sur une ligne est n ! (prononcé 'n factorielle'). n! = n × (n – 1) × (n – 2) ×…× 3 × 2 × 1
Exemple
De combien de manières différentes les lettres P, Q, R, S peuvent-elles être arrangées ?
La réponse est 4 ! = 24.
C'est parce qu'il y a quatre espaces à remplir : _, _, _, _
Le premier espace peut être rempli par l'une des quatre lettres. Le deuxième espace peut être rempli par l'une des 3 lettres restantes. Le troisième espace peut être rempli par l'une des 2 lettres restantes et le dernier espace doit être rempli par la seule lettre restante. Le nombre total d'arrangements possibles est donc de 4 × 3 × 2 × 1 = 4 !
Le nombre de façons d'arranger n objets, parmi lesquels p d'un type sont semblables, q d'un deuxième type sont semblables, r d'un troisième type sont semblables, etc. est :
n! . p! q! r! …
Exemple
De combien de manières les lettres du mot : STATISTIQUES peuvent-elles être disposées ?
Il y a 3 S, 2 I et 3 T dans ce mot, donc le nombre de façons d'arranger les lettres est :
10!=50 400
3! 2! 3!
Anneaux et ronds-points
- Le nombre de façons d'arranger n objets différents dans un anneau lorsque les arrangements dans le sens des aiguilles d'une montre et dans le sens inverse des aiguilles d'une montre sont différents est de (n – 1) !
Lorsque les dispositions dans le sens des aiguilles d'une montre et dans le sens inverse des aiguilles d'une montre sont les mêmes, le nombre de voies est de ½ (n – 1) !
Exemple
Dix personnes vont à une fête. De combien de façons différentes peuvent-ils s'asseoir ?
Les dispositions dans le sens inverse des aiguilles d'une montre et dans le sens des aiguilles d'une montre sont les mêmes. Par conséquent, le nombre total de voies est de ½ (10-1) ! = 181 440
Combinaisons
Le nombre de façons de sélectionner r objets parmi n objets différents est :
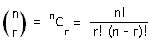
Exemple
Il y a 10 balles dans un sac numérotées de 1 à 10. Trois balles sont tirées au sort. Combien y a-t-il de manières différentes de sélectionner les trois boules ?
10 C 3 = 10 ! = 10 × 9 × 8 = 120
3 ! (10 – 3) !3 × 2 × 1
Permutations
Une permutation est un arrangement ordonné.
Le nombre d'arrangements ordonnés de r objets tirés de n objets différents est :
n P r = n! . (n-r) !
Exemple
Dans la compétition But du mois du match du jour, vous deviez choisir les 3 meilleurs buts sur 10. L'ordre étant important, c'est la formule de permutation que nous utilisons.
10 P 3 = 10 !
7!
= 720
Il y a donc 720 façons différentes de désigner les trois premiers buts.
Probabilité
Les faits ci-dessus peuvent être utilisés pour aider à résoudre des problèmes de probabilité.
Exemple
A la Loterie Nationale, 6 numéros sont choisis parmi 49. Vous gagnez si les 6 boules que vous choisissez correspondent aux 6 boules sélectionnées par la machine. Quelle est la probabilité de gagner à la loterie nationale ?
Le nombre de façons de choisir 6 nombres parmi 49 est 49 C 6 = 13 983 816 .
Par conséquent, la probabilité de gagner à la loterie est de 1/13983816 = 0,000 000 071 5 (3sf), ce qui correspond à environ 1 chance sur 14 millions.


