Théorie de base
Définition
Le processus d'essais de Bernoulli , du nom de Jacob Bernoulli, est l'un des processus aléatoires les plus simples mais les plus importants en probabilité. Essentiellement, le processus est l'abstraction mathématique du tirage au sort, mais en raison de sa large applicabilité, il est généralement énoncé en termes d'une séquence d' essais
génériques .
Une séquence d' essais de Bernoulli satisfait les hypothèses suivantes :
- Chaque essai a deux résultats possibles, dans le langage de la fiabilité appelé succès et échec .
- Les épreuves sont indépendantes. Intuitivement, le résultat d'un essai n'a aucune influence sur le résultat d'un autre essai.
- A chaque essai, la probabilité de succès est et la probabilité d'échec est où est le paramètre de réussite du processus.
Variables aléatoires
Mathématiquement, nous pouvons décrire le processus d'essais de Bernoulli avec une séquence de variables aléatoires indicatrices :
Une variable indicatrice est une variable aléatoire qui ne prend que les valeurs 1 et 0, qui dans ce paramètre indiquent respectivement le succès et l'échec. Variable indicatrice enregistre simplement le résultat du procès . Ainsi, les variables indicatrices sont indépendantes et ont la même fonction de densité de probabilité :
La distribution définie par cette fonction de densité de probabilité est connue sous le nom de distribution de Bernoulli . En termes statistiques, le processus d'essais de Bernoulli correspond à un échantillonnage de la distribution de Bernoulli. En particulier, le premier essais former un échantillon aléatoire de taille de la distribution de Bernoulli. Notons encore que le processus des essais de Bernoulli est caractérisé par un seul paramètre.La fonction de densité de probabilité conjointe de les épreuves sont données par
Preuve
Notez que l'exposant de dans la fonction de densité de probabilité est le nombre de succès dans le essais, tandis que l'exposant de est le nombre d'échecs.
Si est un processus d'essais de Bernoulli avec le paramètre alors est une suite d'essais de Bernoulli de paramètre .
Supposer que est une séquence de variables aléatoires indépendantes, chacune avec la distribution uniforme sur l'intervalle . Pour et , laisser . Puis est un processus d'essais de Bernoulli avec probabilité .
Notez que dans le résultat précédent, les essais de Bernoulli traitent pour toutes les valeurs possibles du paramètre sont définis sur un espace de probabilité commun. Ce type de construction est parfois appelé accouplement . Ce résultat montre également comment simuler un processus d'essais de Bernoulli avec des nombres aléatoires. Tous les autres processus aléatoires étudiés dans ce chapitre sont des fonctions de la séquence d'essais de Bernoulli et peuvent donc également être simulés.
Des moments
Laisser être une variable indicatrice avec , où . Ainsi, est le résultat d'un essai générique de Bernoulli et a la distribution de Bernoulli avec le paramètre . Les résultats suivants donnent la moyenne, la variance et certains des moments les plus élevés. Un fait utile est que si nous prenons une puissance positive d'une variable indicatrice, rien ne se passe ; C'est, pour
La moyenne et la variance de sommes
Preuve
A noter que le graphique de , en tant que fonction de est une parabole s'ouvrant vers le bas. En particulier, la plus grande valeur est lorsque , et la plus petite valeur est 0 lorsque ou . Bien entendu, dans les deux derniers cas, est déterministe, prenant la valeur unique 0 lorsque et la valeur unique 1 lorsque
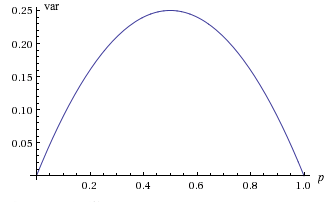
Chiffre : en tant que fonction de
Supposer que . L'asymétrie et l'aplatissement de sommes
La fonction génératrice de probabilité de est pour .
Exemples et applications
Pièces de monnaie
Comme nous l'avons noté précédemment, l'exemple le plus évident des essais de Bernoulli est le tirage au sort, où le succès signifie face et l'échec signifie pile. Le paramètre est la probabilité de face (donc en général, la pièce est biaisée).
Dans l'expérience de base de la pièce, définissez et pour chaque exécuter l'expérience et observer les résultats.
Exemples génériques
Dans un sens, l'exemple le plus général d'essais de Bernoulli se produit lorsqu'une expérience est répliquée. Plus précisément, supposons que nous ayons une expérience aléatoire de base et un événement d'intérêt. Supposons maintenant que nous créions une expérience composée qui consiste en des réplications indépendantes de l'expérience de base. Définir le succès à l'essai signifier cet événement s'est produit le th run, et définir l'échec à l'essai signifier cet événement ne s'est pas produit le e course. Ceci définit clairement un processus d'essais de Bernoulli avec le paramètre.
Des essais de Bernoulli sont également formés lorsque nous échantillonnons à partir d'une population dichotomique. Plus précisément, supposons que nous ayons une population de deux types d'objets, que nous appellerons type 0 et type 1. Par exemple, les objets pourraient être des personnes, classées comme hommes ou femmes , ou les objets pourraient être des composants, classés comme bon ou défectueux . Nous sélectionnonsobjets au hasard parmi la population; par définition, cela signifie que chaque objet de la population au moment du tirage est également susceptible d'être choisi. Si l'échantillonnage est avec remise , alors chaque objet tiré est remplacé avant le prochain tirage. Dans ce cas, les tirages successifs sont indépendants, de sorte que les types des objets de l'échantillon forment une séquence d'essais de Bernoulli, dans laquelle le paramètreest la proportion d'objets de type 1 dans la population. Si l'échantillonnage est sans remise , alors les tirages successifs sont dépendants, de sorte que les types des objets de l'échantillon ne forment pas une séquence d'essais de Bernoulli. Cependant, si la taille de la population est grande par rapport à la taille de l'échantillon, la dépendance causée par le non-remplacement des objets peut être négligeable, de sorte qu'à toutes fins pratiques, les types d'objets dans l'échantillon peuvent être traités comme une séquence d'essais de Bernoulli. . Une discussion supplémentaire sur l'échantillonnage à partir d'une population dichotomique se trouve dans le chapitre Modèles d'échantillonnage fini.
Supposons qu'un élève passe un test à choix multiples. Le test comporte 10 questions, chacune ayant 4 réponses possibles (une seule correcte). Si l'élève devine aveuglément la réponse à chaque question, les questions forment-elles une séquence d'essais de Bernoulli ? Si oui, identifiez les résultats de l'essai et le paramètre.
Réponse
Candidat est candidat à un poste dans un certain district. Vingt personnes sont choisies au hasard parmi la population des électeurs inscrits et invitées à choisir leur candidat. Les réponses forment-elles une séquence d'essais de Bernoulli ? Si oui, identifiez les résultats de l'essai et la signification du paramètre.
Réponse
Une roue de roulette américaine a 38 emplacements ; 18 sont rouges, 18 sont noirs et 2 sont verts. Un joueur joue à la roulette 15 fois, en pariant à chaque fois sur le rouge. Les résultats forment-ils une séquence d'essais de Bernoulli ? Si oui, identifiez les résultats de l'essai et le paramètre.
Réponse
La roulette est abordée plus en détail dans le chapitre sur les jeux de hasard.
Deux joueurs de tennis jouent un ensemble de 6 jeux. Les jeux forment-ils une séquence d'épreuves de Bernoulli ? Si oui, identifiez les résultats de l'essai et la signification du paramètre.
Réponse
Fiabilité
Rappelons que dans le modèle standard de fiabilité structurelle, un système est composé de composants qui fonctionnent indépendamment les uns des autres. Laisser désigne l'état du composant , où 1 signifie fonctionner et 0 signifie échec. Si les composants sont tous du même type, alors notre hypothèse de base est que le vecteur d'état
est une séquence d'essais de Bernoulli. L'état du système, (là encore où 1 signifie fonctionner et 0 signifie échoué) ne dépend que de l'état des composants, et est donc une variable aléatoireoù est la fonction de structure . Généralement, la probabilité qu'un appareil fonctionne est la fiabilité de l'appareil, donc le paramètrede la séquence d'essais de Bernoulli est la fiabilité commune des composants. Par indépendance, la fiabilité du système est fonction de la fiabilité du composant :où nous soulignons la dépendance de la mesure de probabilité sur le paramètre . Assez convenablement, cette fonction est connue sous le nom de fonction de fiabilité . Notre défi est généralement de trouver la fonction de fiabilité, étant donné la fonction de structure.Un système en série fonctionne si et seulement si chaque composant fonctionne.
- L'état du système est .
- La fonction de fiabilité est pour .
Un système parallèle fonctionne si et seulement si au moins un composant fonctionne.
- L'état du système est .
- La fonction de fiabilité est pour .
Rappelons que dans certains cas, le système peut être représenté sous forme de graphe ou de réseau . Les arêtes représentent les composants et les sommets les connexions entre les composants. Le système fonctionne si et seulement s'il existe un chemin de travail entre deux sommets désignés, que nous désignerons par et .
Trouvez la fiabilité du réseau de ponts de Wheatstone illustré ci-dessous (du nom de Charles Wheatstone).
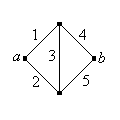
Chiffre : Le réseau du pont de Wheatstone
Réponse
Le test sanguin poolé
Supposons que chaque personne d'une population, indépendamment de toutes les autres, souffre d'une certaine maladie avec une probabilité . Ainsi, vis-à-vis de la maladie, les personnes de la population forment une séquence d'essais de Bernoulli. La maladie peut être identifiée par un test sanguin, mais bien sûr le test a un coût.
Pour un groupe de personnes, nous comparerons deux stratégies. La première consiste à tester le personnes individuellement, de sorte que, bien sûr, des tests sont nécessaires. La deuxième stratégie consiste à mettre en commun les échantillons de sang despersonnes et tester d'abord l'échantillon regroupé. On suppose que le test est négatif si et seulement si tousles personnes sont indemnes de la maladie ; dans ce cas, un seul test est requis. En revanche, le test est positif si et seulement si au moins une personne est atteinte de la maladie, auquel cas il faut alors tester les personnes individuellement ; dans ce casdes tests sont nécessaires. Ainsi, laissez désignent le nombre de tests requis pour la stratégie groupée.
Le nombre d'épreuves a les propriétés suivantes :
En termes de valeur attendue, la stratégie groupée est meilleure que la stratégie de base si et seulement si
Le graphique de la valeur critique en tant que fonction de est représenté dans le graphique ci-dessous :
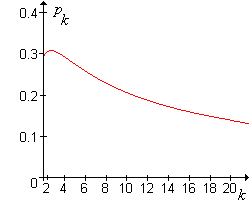
Chiffre : Le graphique de en tant que fonction de
La valeur critique satisfait les propriétés suivantes :
- La valeur maximale de se produit à et .
- comme .
Il s'ensuit que si , la mutualisation n'a jamais de sens, quelle que soit la taille du groupe . A l'autre extrême, si est très petite, de sorte que la maladie est assez rare, la mise en commun est meilleure sauf si la taille du groupe est très grand.
Supposons maintenant que nous ayons personnes. Si alors nous pouvons diviser la population en groupes de chacun, et appliquer la stratégie groupée à chaque groupe. Noter que correspond à des tests individuels, et correspond à la stratégie mutualisée sur l'ensemble de la population. Laisser désigne le nombre de tests requis pour le groupe .
Les variables aléatoires sont indépendants et chacun a la distribution donnée ci-dessus .
Le nombre total de tests requis pour ce schéma de partitionnement est .
Le nombre total de tests attendu est
La variance du nombre total de tests est
Ainsi, en termes de valeur attendue, la stratégie optimale consiste à regrouper la population en groupes de taille , où minimise la fonction de valeur attendue ci-dessus. Il est difficile d'obtenir une expression fermée pour la valeur optimale de, mais cette valeur peut être déterminée numériquement pour des et .
Pour les valeurs suivantes de et , trouver la taille de pooling optimale et le nombre prévu de tests. (Restreindre votre attention aux valeurs de qui divise .)
- ,
- ,
- ,
Réponse
Si ne divise pas , alors nous pourrions diviser la population de personnes en groupes de chacun et un groupe restant
avecmembres. Cela complique clairement l'analyse, mais n'introduit pas d'idées nouvelles, nous laisserons donc cette extension au lecteur intéressé.


