- Facilité avec l'algèbre de base, en particulier l'expansion des parenthèses et la collecte de termes similaires.
- LCM et HCF pour l'arithmétique.
La maîtrise de l'algèbre est un outil essentiel pour comprendre et être à l'aise avec les mathématiques. Pour les étudiants qui ont l'intention d'étudier les mathématiques supérieures au-delà du niveau général, la factorisation est une compétence importante qui est fréquemment requise pour résoudre des problèmes plus difficiles et comprendre les concepts mathématiques.
En arithmétique, trouver le HCF ou le LCM de deux nombres, qui était si souvent utilisé pour travailler avec des fractions, des pourcentages et des rapports, impliquait de connaître les facteurs des nombres impliqués. Ainsi, la factorisation des nombres était très utile pour résoudre toute une série de problèmes.
De même en algèbre, la factorisation est un outil remarquablement puissant, qui est utilisé à tous les niveaux. Il fournit une méthode standard pour résoudre des équations quadratiques ainsi, bien sûr, que pour simplifier des expressions compliquées. Il est également utile lors de la représentation graphique des fonctions.
L'affacturage (ou factorisation ) est le contraire de l'expansion. Ainsi, en utilisant la loi de distribution,
3( x − 2) est la forme factorisée de 3 x − 6, et ( x − 1)( x + 6) est la factorisée dex 2 + 5 x − 6.
Bien que l'expansion soit relativement routinière, la factorisation peut être délicate et l'étudiant aura besoin de beaucoup de pratique pour maîtriser les différents types de factorisation qui se présentent, ainsi que pour avoir un aperçu des méthodes à appliquer et de la maîtrise de leur application.
Le type d'affacturage le plus simple consiste à extraire un facteur commun de deux termes ou plus.
Par exemple, chaque terme de l'expression 6 x 2 y − 4 x est divisible par 2 et par x . Ainsi, 2 x est un facteur commun. Puisqu'il n'y a pas d'autre facteur commun, 2 x est le facteur commun le plus élevé. Nous divisons chaque terme par et voyons ce qui reste. Ainsi,
6 x 2 y − 4 x = 2 x (3 xy − 2).
Les termes de l'expression entre parenthèses n'ont pas de facteur commun (sauf 1) et cette expression ne peut donc pas être factorisée davantage.
La suppression des facteurs communs peut également être effectuée sur plus de deux termes.
EXEMPLE
Facteur 6 a 2 b − 8 ab + 10 ab 2 .
SOLUTION
Le plus grand facteur commun des trois termes est 2 ab donc
6 a 2 b − 8 ab + 10 ab 2 = 2 ab (3 ab − 4 + 5 b )
Dans certains cas, il peut n'y avoir aucun facteur commun à tous les termes d'une expression donnée. Il peut cependant être utile de factoriser par paires.
Par exemple, il n'y a pas de facteur commun aux quatre termes de l'expression
2 a 2 + 3 ab + 4 + 6 b,
cependant, les deux premiers termes ont un facteur commun d' un tandis que les deux seconds ont un facteur commun de 2. Ainsi,
2 a 2 + 3 ab + 4 a + 6 b = a (2 a + 3 b ) + 2(2 a + 3 b ).
Nous pouvons maintenant voir que les deux termes résultants ont un facteur commun de qui peut maintenant être factorisé pour produire (2 a + 3 b )( a + 2).
| D'où | | 2 a 2 + 3 ab + 4 a + 6 b | = a (2 a + 3 b ) + 2(2 a + 3 b ) |
| = (2 a + 3 b )( a + 2). |
Notez que l'ordre dans lequel les parenthèses sont écrites et l'ordre des termes entre parenthèses n'ont pas d'importance.
Les étudiants auront besoin d'un peu de pratique avec cette méthode, en particulier avec la deuxième étape.
EXEMPLE
Facteur 3 a 2 − 5 ac − 3 ab + 5 cb.
SOLUTION
| 3 a 2 − 5 ac − 3 ab + 5 cb | = a (3 a − 5 c ) − b (3 a − 5 c ) | | |
| = a (3 a − 5 c ) − b (3 a − 5 c ) | (Notez que nous factorisons pour obtenir le prochain facteur commun.) | ||
| = (3 a − 5 c )( a − b ) | (Sortez le facteur commun). |
Remarque : un appariement différent de termes peut ou non conduire à une factorisation utile. Ainsi, dans l'exemple ci-dessus, l'appariement de 3 a 2 − 5 ac − 3 ab + 5 cb conduit à 3 a ( a − b ) − 5 b ( a − b ) comme précédemment. Cependant l'appariement des termes comme (3 a 2 + 5 cb ) − 5 ac − 3 ab ne conduit pas à une factorisation.
La factorisation peut nous donner des informations utiles concernant une expression comme le
montre l'exercice suivant .
EXERCICE 1
Factoriser l'expression xy − 5 x − 2 y + 10 et énoncer des conditions sur x , y telles que lorsque des valeurs numériques sont substituées à x et y l'expression donnée
a
est égal à 0, 
b est positif, c est négatif.
Il y a trois développements spéciaux et factorisations correspondantes qui se produisent fréquemment en algèbre.
Le premier d'entre eux est une identité connue sous le nom de différence de carrés. Une identité est une déclaration en algèbre qui est vraie pour toutes les valeurs des pronuméraux.
En développant, il est facile de montrer que
( x − y )( x + y ) = x 2 − y 2 .
La différence entre les carrés de deux nombres est donc égale à leur somme multipliée par leur différence.
EXEMPLE
Facteur a c 2 − 25 b 16 a 2 − 9 y 2 .
SOLUTION
a c 2 − 25 = ( c − 5)( c + 5) b 16 a 2 − 9 y 2 = (4 a + 3 y )(4 a − 3 y )
(Comme d'habitude, l'ordre dans lequel les facteurs sont écrits n'a pas d'importance.)
Cette identité peut être utilisée pour simplifier des expressions algébriques.
EXEMPLE
Simplifier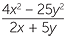 
.
SOLUTION
= 
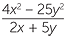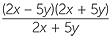= 2 x − 5 y .
Il existe un certain nombre d'applications utiles pour compléter le carré.
Une de ces applications est le calcul mental. Par exemple, pour multiplier disons 13 et 15,
nous écrivons le produit sous la forme 13 × 15 = (14 − 1)(14 + 1) = 14 2 − 1 = 195.
Avec de la pratique, cela peut être fait mentalement, à condition que les carrés des nombres entiers jusqu'à environ
20 soient connus.
La différence de deux carrés peut aussi être utilisée pour résoudre des équations dans lesquelles on ne cherche que des solutions entières.
EXEMPLE
Trouvez toutes les solutions entières positives de x 2 − 9 y 2 = 13.
SOLUTION
En factorisant le membre de gauche, nous avons ( x − 3 y )( x + 3 y ) = 13
Parce que x et y sont positifs, il s'ensuit que x + 3 y et x − 3 y sont donc positifs puisque leur produit est 13.
Les seuls facteurs positifs de 13 sont 13 et 1, nous avons donc les deux cas :
( x − 3 y ) = 1 et ( x + 3 y ) = 13 L'addition donne donc 2 x = 14 donc x = 7. En remplaçant, nous obtenons y = 2. | | ( x − 3 y ) = 13 et ( x + 3 y ) = 1 L'addition donne donc 2 x = 14 donc x = 7. En resubstituant, nous obtenons y = −2. |
Puisque nous ne voulons que des solutions entières positives, nous concluons que la seule solution entière positive à x 2 − 9 y 2 = 13 est x = 7, y = 2.
Les deux autres extensions spéciales mentionnées ci-dessus sont les identités :
a 2 + 2 ab + b 2 = ( a + b ) 2 et a 2 − 2 ab + b 2 = ( a − b ) 2 .
Ces identités sont plus difficiles à utiliser que la différence de deux carrés et sont probablement
mieux traitées comme des cas particuliers de factorisation quadratique, discutés ci-dessous. Ainsi, par exemple, il n'est pas facile pour les élèves de repérer rapidement que 4 x 2 − 12 xy + 9 y 2 est un carré parfait égal à(2 x − 3 y ) 2 .
L'exemple suivant montre comment ces idées peuvent être astucieusement combinées pour factoriser une expression qui, à première vue, ne semble pas prendre en compte.
Reconnaître des exemples simples de carrés parfaits est une compétence utile.
EXEMPLE
Facteur x 4 + 4.
SOLUTION
À première vue, cette expression ne semble pas prendre en compte, car il n'y a pas d'identité pour la somme des carrés.
Cependant, en ajoutant et en soustrayant le terme , nous arrivons à une différence de carrés.
| x 4 + 4 | = ( x 4 + 4 x 2 + 4) − 4 x 2 |
| = ( x 2 + 2) 2 − (2 x ) 2 (La première parenthèse est un carré parfait) | ||
| = (( x 2 + 2) − 2 x )(( x 2 + 2) − 2 x ) | ||
| = ( x 2 − 2 x + 2)( x 2 + 2 x + 2) |
Un quadratique monique est une expression de la forme x 2 + bx + c , où et sont donnés des nombres.
Lorsque nous développons, par exemple, ( x + 2)( x + 5), nous obtenons
| ( x + 2)( x + 5) | = x ( x + 5) + 2( x + 5) |
| = x 2 + 5 x + 2 x + 10 | ||
| = x 2 + 7 x + 10. |
Ce développement produit un simple quadratique. Nous aimerions trouver une procédure qui inverse ce processus.
On remarque que le coefficient x de est la somme des deux nombres 2 et 5 entre parenthèses et que le terme constant 10, est le produit de 2 et 5. Ceci suggère une méthode de factorisation.
En général, quand on développe ( x + α)( x + β), on obtient
( x + )( x + β) = x 2 +α x + βx + αβ = x 2 + (α + β) x + .
Le coefficient de x est α + β et le terme constant est . Donc pour inverser le processus, on cherche deux nombres dont la somme est le coefficient de et dont le produit est le terme constant.
EXEMPLE
Facteur x 2 + 7 x + 12.
SOLUTION
Nous cherchons à exprimer cela sous la forme ( x + α)( x + β). Pour trouver les valeurs d' un et b , nous résolvons, par inspection, α + β = 7 et αβ = 12. Il est clair que les solutions sont 4 et 3 (dans un ordre), et aucun autre nombre de ces équations satisfont. D'où
x 2 + 7 x + 12 = ( x + 4)( x + 3).
Notez que l'ordre dans lequel nous écrivons les parenthèses est sans importance.
Les élèves doivent essayer de se développer mentalement pour vérifier que leurs réponses sont correctes.
EXEMPLE
Facteur a x 2 − 7 x + 12 b x 2 + 2 x − 15 c x 2 + 6 x + 9
SOLUTION
- une
- On résout, par inspection, α + β = −7 et α β = 12.
Les solutions sont −4 et −3. D'où
x 2 − 7 x + 12 = ( x − 4)( x − 3). - b
- On résout, par inspection, α + β = 2 et α β = −15. Les solutions sont 5 et -3. Donc
x 2 + 2 x − 15 = ( x + 5)( x − 3). - c
- On résout, par inspection, α + β = 6 et α β = 9. Les solutions sont 3 et 3. Donc
x 2 + 6 x + 9 = ( x + 3)( x + 3) = ( x + 3) 2 .
Notez que dans c la réponse est un carré parfait.
Notez également que la factorisation des différences de carrés pourrait également être effectuée en utilisant cette méthode. Par exemple, pour factoriser x 2 − 16, on résout α + β = 0 et αβ = −16. Les solutions sont 4 et −4 travail, donc x 2 − 16 = ( x − 4)( x + 4).
Ce n'est cependant pas une bonne méthode à utiliser. Il est préférable pour les étudiants d'être attentifs à la différence d'identité des carrés et de l'appliquer directement.
Les étudiants auront besoin de beaucoup de pratique avec la factorisation quadratique. Il convient de mentionner ici que dans les mathématiques plus poussées, à la fois dans les années supérieures et tout au long des mathématiques de niveau tertiaire, des expressions quadratiques apparaissent régulièrement et donc être capable de les factoriser rapidement est une compétence de base.
QUADRATIQUES AVEC DES FACTEURS COMMUNS
Nous devons toujours être à l'affût des facteurs communs avant d'utiliser d'autres
techniques d'affacturage.
Par exemple, pour factoriser 3 x 2 + 9 x + 6, nous commençons par retirer le facteur commun 3. Nous pouvons ensuite continuer à factoriser. Ainsi,
| 3 x 2 + 9 x + 6 | = 3( x 2 + 3 x + 2) |
| = 3( x + 2)( x + 1) |
EXERCICE 2
Facteur 6 x 2 − 54.
Nous avons dit plus haut qu'un quadratique monique est une expression de la forme x 2 + bx + c ,
où b et c sont des nombres donnés. Un quadratique non monique est une expression de la forme ax 2 + bx + c , où a , b et c sont des nombres donnés, et a ≠ 1 ou 0.
Ainsi, par exemple, 2 x 2 + 5 x + 3 est un exemple de quadratique non monique.
Il existe différentes techniques pour factoriser ce type d'expression. Celui présenté ici est considéré comme le plus facile à exécuter et à expliquer. Il est également lié aux techniques décrites ci-dessus. Il y a trois étapes dans la méthode, qui seront illustrées sur l'exemple 2 x 2 + 5 x + 3.
- Étape 1
- Multipliez le coefficient de par le terme constant et écrivez-le au-dessus du terme constant
| 6 | |
| 2 x 2 + 5 x + | 3 |
- Étape 2
- Trouvez deux nombres qui s'additionnent pour donner le coefficient de et multipliez pour donner ce nouveau produit. C'est-à-dire deux nombres qui s'additionnent pour donner 5 et se multiplient pour donner 6. Les nombres 3 et 2 fonctionnent.
- Étape 3
- Utilisez ces nombres pour diviser le moyen terme et factoriser par paires.
| 2 x 2 + 5 x + 3 | = 2 x 2 + 2 x + 3 x + 3 |
| = 2 x ( x + 1) + 3( x + 1) | ||
| = ( x + 1) (2 x + 3). |
Ces étapes sont précisément le processus inverse de l'expansion.
Peu importe dans quel ordre nous écrivons les termes intermédiaires, la méthode fonctionnera toujours, donc
| 2 x 2 + 5 x + 3 | = 2 x 2 + 3 x + 2 x + 3 |
| = x (2 x + 3) + 1 (2 x + 3) | ||
| = ( x + 1) (2 x + 3). |
EXEMPLE
Facteur 3 x 2 + 5 x − 2.
SOLUTION
| 3 x 2 + 5 x − 2 | | (3 × (−2 )= −6) | |
| 3 x 2 + 5 x − 2 | = 3 x 2 + 6 x − x −2 | |||
| = 3 x ( x + 2) −( x + 2) | (6 − 1 = 5, 6 × (−1) = −6) | |||
| = 3 x ( x + 2) -1( x + 2) | ||||
| = ( x + 2) (3 x − 1) |
Soit une expression à deux termes :
- rechercher un facteur commun
- chercher une différence de carrés
Soit une expression à trois termes :
- rechercher un facteur commun
- facteur utilisant la méthode des quadratiques moniques
- facteur utilisant la méthode des quadratiques non moniques
Soit une expression à quatre termes :
- rechercher un facteur commun
- essayez de vous regrouper par paires.
SIMPLIFIER LES EXPRESSIONS ALGÉBRIQUES
Nous allons maintenant appliquer les différentes techniques de factorisation pour simplifier diverses expressions algébriques. Les étudiants doivent faire très attention lors de l'annulation. Les fausses annulations telles que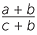 
= 
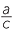sont des erreurs courantes des élèves lorsqu'il s'agit de fractions algébriques. Ils ne doivent pas confondre cela avec l'annulation 
= 
.
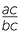EXEMPLE
Simplifier
a b × c ÷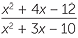 
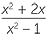
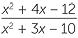
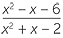
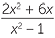
SOLUTION
| une | |  | =  |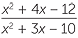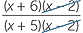
=  |
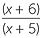| b | |  ×  | =  × |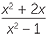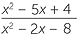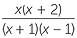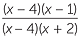
=  | |||
=  |
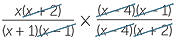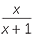| c | | Inversez et multipliez avant de factoriser. | |
 ??  | =  × | ||
= ×   | |||
=  | |||
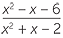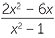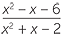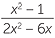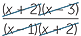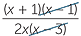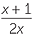La factorisation peut également nous aider à trouver le plus petit dénominateur commun lors de l'addition ou de la soustraction de fractions algébriques.
EXEMPLE
Simplifier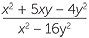 
- 
.
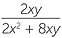SOLUTION
 −  | =  - |
=  - | |
=  | |
=  | |
=  . |
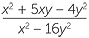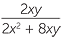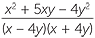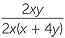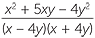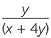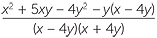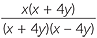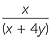La factorisation quadratique fournit l'une des méthodes clés pour résoudre les équations quadratiques. De telles équations apparaissent naturellement et fréquemment dans presque tous les domaines des mathématiques.
La méthode de résolution repose sur le simple fait que si nous obtenons zéro comme produit de deux nombres, alors au moins un des nombres doit être zéro.
Autrement dit, si ab = 0 alors a = 0 ou b = 0.
Par conséquent, pour résoudre x 2 − 7 x + 12 = 0, nous factorisons le quadratique comme ( x − 4)( x − 3) = 0 et concluons que ( x − 4) = 0 ou ( x − 3) = 0.
Ces équations peuvent être facilement résolues pour donner x = 3 ou x = 4.
La méthode de factorisation des quadratiques non-moniques peut également être utilisée pour résoudre des équations quadratiques non-moniques.
EXEMPLE
Résoudre 3 x 2 + 5 x − 2 = 0.
SOLUTION
3 x 2 + 5 x − 2 = 0
(3 x − 1)( x + 2) = 0
3 x − 1 = 0 ou x + 2 = 0
Donc, x =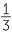 
ou x = −2.
On notera que toutes les équations quadratiques n'ont pas de solutions rationnelles. Ces équations ne se prêtent pas à la méthode de factorisation.
D'autres techniques seront développées dans le module Equations quadratiques pour traiter de
telles équations.
La différence d'identité des carrés discutée ci-dessus peut être généralisée aux cubes.
En développant le membre de droite, on montre que
a 3 − b 3 = ( a − b )( a 2 + ab + b 2 ) et a 3 + b 3 = ( a + b )( a 2 − ab + b 2 ).
Ces identités sont appelées respectivement différence de cubes et somme de cubes . Dans les deux cas, le facteur dans la deuxième parenthèse peut être rappelé comme "carré le premier, carré le second, multiplier et changer le signe".
Ces identités sont généralement couvertes en mathématiques supérieures et sont utiles pour commencer le calcul et pour trouver des limites.
La différence de carrés et la différence de cubes peuvent être encore généralisées pour obtenir une factorisation de a n − b n .
En développant le membre de droite, on montre que
a n − b n = ( a − b )( a n −1 + a n −2 b + a n −3 b 2 + … + ab n −2 + b n −1 )
Comme cas particulier, notons que
x n − 1 = ( x − 1)( x n −1 + x n −2 + x n −3 + … + x + 1).
EXERCICE 3
- une
- En développant, vérifiez chacune de ces identités.
- b
- Vérifiez que nous obtenons la différence et les carrés et les cubes, lorsque nous remplaçons
n par 2 et 3. - c
- Facteur x 4 − 1 à la fois en utilisant l'identité ci-dessus et aussi en utilisant la différence de carrés. Comparez les deux factorisations.
Bien qu'il n'y ait pas de « somme de carrés », la somme des cubes admet une généralisation.
Si nous utilisons des indices impairs, nous trouvons que
x 5 + 1 = ( x + 1)( x 4 − x 3 + x 2 − x + 1) et
x 7 + 1 = ( x + 1)( x 6 − x 5 + x 4 − x3 + x 2 − x + 1), et ainsi de suite.
EXERCICE 4
Ecrire et vérifier par développement, la factorisation de x 2 n +1 + 1.
Des expressions telles que x 3 − 6 x 2 + 3 x − 1 sont appelées polynômes . Puisque la plus grande puissance de x dans l'expression est 3, nous appelons cela un polynôme de degré 3, ou un cube . Les polynômes seront discutés plus en détail dans le module Polynômes .
Il existe des méthodes pour factoriser de telles expressions. Parfois, il est impossible de factoriser un polynôme en facteurs linéaires à l'aide de nombres rationnels, mais il peut être possible de factoriser une expression contenant des termes de degré 6 par exemple dans un produit contenant des termes de x 3 . Par exemple, x 6 − x 4 + 2 x 3 − 2 x + 2 peut, avec une certaine difficulté, être factorisé comme ( x 3 + 2)( x 3 − x + 1). Les expressions dans chaque parenthèse ne peuvent pas être davantage factorisées en utilisant uniquement des nombres rationnels. On dit que ces facteurs sont irréductibles sur les nombres rationnels .
Il existe des expressions irréductibles sur les nombres rationnels, mais qui peuvent être factorisées si l'on admet les nombres irrationnels. Par exemple, le polynôme x 4 + 1 ne peut pas être factorisé en utilisant des nombres rationnels, mais il peut être factorisé en utilisant une méthode similaire à celle donnée à la page 5 comme ( x 2 + 
x + 1)( x 2 − 
x + 1). Ceci peut être vérifié par expansion. Nous appelons cela une factorisation sur les nombres réels .
Les élèves qui étudient les nombres complexes en mathématiques supérieures découvriront que :
- sur les nombres complexes, chaque polynôme peut être factorisé en un produit de facteurs linéaires,
- sur les nombres réels, chaque polynôme peut être factorisé en un produit de facteurs linéaires et/ou quadratiques.
Sur les nombres rationnels, il est possible de trouver des polynômes, de degré aussi grand que l'on veut, qui soient irréductibles. Par exemple, x 6 + x 5 + x 4 + x 3 + x 2 + x + 1 peut être montré irréductible sur les nombres rationnels.
L'affacturage fait partie de l'algèbre et son histoire appartient donc à l'histoire de l'algèbre couverte dans d'autres modules.
Les questions de factorisation et de développement de méthodes de factorisation, à un niveau plus avancé, faisaient partie des travaux de grands mathématiciens tels que Gauss (1777-1855), Galois (1811-1832) et Abel (1802-1829). C'est Gauss qui a donné le premier la preuve que les polynômes peuvent être complètement factorisés en facteurs linéaires sur les nombres complexes.
Les polynômes qui résultent de la factorisation de x n − 1 sur les nombres entiers sont appelés polynômes cyclotomiques et ont également été étudiés par ces mathématiciens et plus tard. Par exemple, depuisx 3 − 1 = ( x − 1)( x 2 + x + 1)le polynôme x 2 + x + 1 est un exemple de polynôme cyclotomique. Ces polynômes ont des propriétés intéressantes et il y a un certain nombre de problèmes non résolus les concernant.
L'une des nombreuses applications de la factorisation, qui remonte aux Grecs, est la résolution d'équations dans lesquelles on ne cherche que des solutions entières (parfois des entiers positifs). De telles équations sont appelées équations diophantiennes . Ceux-ci utilisent parfois des factorisations astucieuses.
EXEMPLE
Trouvez toutes les solutions entières positives de ab + 2 a + 5 b = 38.
SOLUTION
Les deux premiers termes se factorisent en a ( b + 2). Nous ajoutons 10 des deux côtés, afin que nous puissions prendre en compte les paires. Ainsi,
| ab + 2 a + 5 b | = 38 |
| ab + 2 a + 5 b + 10 | = 48 | |
| a ( b + 2) + 5( b + 2) | = 48 | |
| ( a + 5)( b + 2) | = 48 |
En assimilant chaque parenthèse à un facteur et un cofacteur 48 et en résolvant, nous trouvons que les seules solutions entières positives sont a = 11, b = 1 ; a = 1, b = 6; a = 3, b = 4 ; a = 7, b = 2.
EXERCICE 5
Vérifiez toutes les étapes de l'exemple ci-dessus, puis recherchez également toutes les solutions entières.
EXERCICE 1
a x = 2 ou y = 5 b x > 2 et y > 5 ou x < 2 et y < 5
c x > 2 et y < 5 ou x < 2 et y > 5
EXERCICE 2
6( x − 3)( x + 3)
EXERCICE 4
x 2 n + 1 + 1 = ( x + 1)( x 2 n − x 2 n −1 + x 2 n … + x 2 − x + 1)
EXERCICE 5
a = −17, b = − 6; a = -9, b = -14; a = -8, b = -18; a = −21, b = − 5; a = -7, b = - 26;
a = -29, b = - 4; a = -11, b = -10; a = −13, b = − 8; a = -6, b = - 50; a = -4, b = - 46;
a = 43, b = − 1 ; a = − 3, b = 22; une=19, b = 0 ; a = -1, b = 10; a = 7, b = 2 ; a = -2, b = 14.