On peut dire sans risque de se tromper que la plupart des utilisateurs de statistiques connaissent mieux les analyses paramétriques que les analyses non paramétriques. Les tests non paramétriques sont également appelés tests sans distribution car ils ne supposent pas que vos données suivent une distribution spécifique.
Vous avez peut-être entendu dire que vous devriez utiliser des tests non paramétriques lorsque vos données ne répondent pas aux hypothèses du test paramétrique, en particulier l'hypothèse concernant les données normalement distribuées. Cela semble être une façon simple et agréable de choisir, mais il y a des considérations supplémentaires.
Dans cet article, je vais vous aider à déterminer quand vous devez utiliser un :
- Analyse paramétrique pour tester les moyennes des groupes.
- Analyse non paramétrique pour tester les médianes des groupes.
En particulier, je me concentrerai sur une raison importante d'utiliser des tests non paramétriques qui, à mon avis, n'est pas assez souvent mentionnée !
TESTS D'HYPOTHÈSE DE LA MOYENNE ET DE LA MÉDIANE
Les tests non paramétriques sont comme un univers parallèle aux tests paramétriques. Le tableau présente les paires de tests d'hypothèses connexes proposés par Minitab Statistical Software .
Tests paramétriques (moyens) | Tests non paramétriques (médianes) |
test t à 1 échantillon | 1 échantillon Sign, 1 échantillon Wilcoxon |
test t à 2 échantillons | Test de Mann Whitney |
ANOVA à un facteur | Kruskal-Wallis, test médian de Mood |
DOE factoriel avec un facteur et une variable de blocage | essai de Friedman |
RAISONS D'UTILISER DES TESTS PARAMÉTRIQUES
Raison 1 : les tests paramétriques peuvent bien fonctionner avec des distributions asymétriques et non normales
Cela peut être une surprise, mais les tests paramétriques peuvent donner de bons résultats avec des données continues qui ne sont pas normales si vous respectez les directives de taille d'échantillon dans le tableau ci-dessous. Ces directives sont basées sur des études de simulation menées par des statisticiens de Minitab. Pour en savoir plus sur ces études, lisez nos Technical Papers .
Parametric analyses | Directives relatives à la taille de l'échantillon pour les données non normales |
test t à 1 échantillon | Supérieur à 20 |
test t à 2 échantillons | Chaque groupe doit être supérieur à 15 |
ANOVA à un facteur |
|
Raison 2 : les tests paramétriques peuvent donner de bons résultats lorsque la répartition de chaque groupe est différente
Bien que les tests non paramétriques ne supposent pas que vos données suivent une distribution normale, ils ont d'autres hypothèses qui peuvent être difficiles à respecter. Pour les tests non paramétriques qui comparent des groupes, une hypothèse commune est que les données de tous les groupes doivent avoir la même étendue (dispersion). Si vos groupes ont une répartition différente, les tests non paramétriques peuvent ne pas fournir de résultats valides.
D'un autre côté, si vous utilisez le test t à 2 échantillons ou l'ANOVA à un facteur, vous pouvez simplement accéder à la sous- boîte de dialogue Options et décocher Assume des variances égales . Voilà, vous êtes prêt à partir même lorsque les groupes ont des spreads différents !
Raison 3 : Puissance statistique
Les tests paramétriques ont généralement plus de puissance statistique que les tests non paramétriques. Ainsi, vous êtes plus susceptible de détecter un effet significatif lorsqu'il existe vraiment.
RAISONS D'UTILISER DES TESTS NON PARAMÉTRIQUES
Raison 1 : Votre domaine d'études est mieux représenté par la médiane
C'est ma raison préférée d'utiliser un test non paramétrique et celle qui n'est pas assez souvent mentionnée ! Le fait que vous puissiez effectuer un test paramétrique avec des données non normales n'implique pas que la moyenne soit la statistique que vous souhaitez tester.
Par exemple, le centre d'une distribution asymétrique, comme le revenu, peut être mieux mesuré par la médiane où 50 % sont au-dessus de la médiane et 50 % en dessous. Si vous ajoutez quelques milliardaires à un échantillon, la moyenne mathématique augmente considérablement même si le revenu d'une personne type ne change pas.
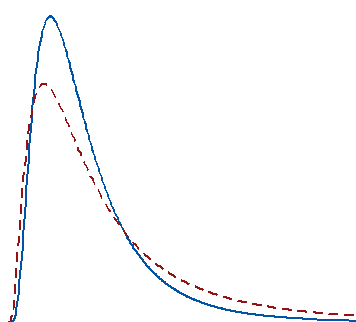
Lorsque votre distribution est suffisamment asymétrique, la moyenne est fortement affectée par des changements très éloignés dans la queue de la distribution, tandis que la médiane continue de refléter plus étroitement le centre de la distribution. Pour ces deux distributions, un échantillon aléatoire de 100 de chaque distribution produit des moyennes significativement différentes, mais des médianes qui ne sont pas significativement différentes.
Deux autres articles de blog illustrent bien ce point :
- Utiliser la moyenne dans l'analyse des données : ce n'est pas toujours un slam-dunk
- L'économie non paramétrique : que signifie réellement la moyenne ?
Raison 2 : vous avez une très petite taille d'échantillon
Si vous ne respectez pas les directives de taille d'échantillon pour les tests paramétriques et que vous n'êtes pas sûr d'avoir des données normalement distribuées, vous devez utiliser un test non paramétrique. Lorsque vous avez un très petit échantillon, vous ne pourrez peut-être même pas déterminer la distribution de vos données, car les tests de distribution manqueront de puissance suffisante pour fournir des résultats significatifs.
Dans ce scénario, vous êtes dans une situation difficile sans alternative valable. Les tests non paramétriques ont moins de puissance au départ et c'est un double coup dur lorsque vous ajoutez une petite taille d'échantillon en plus !
Raison 3 : vous avez des données ordinales, des données classées ou des valeurs aberrantes que vous ne pouvez pas supprimer
Les tests paramétriques typiques ne peuvent évaluer que des données continues et les résultats peuvent être considérablement affectés par les valeurs aberrantes. Inversement, certains tests non paramétriques peuvent gérer des données ordinales, des données classées et ne pas être sérieusement affectés par les valeurs aberrantes. Assurez-vous de vérifier les hypothèses du test non paramétrique, car chacun a ses propres exigences en matière de données.
Si vous avez des données Likert et que vous souhaitez comparer deux groupes, lisez mon article Best Way to Analyze Likert Item Data: Two Sample T-Test versus Mann-Whitney .
PENSÉES DE CLÔTURE
On pense généralement que le besoin de choisir entre un test paramétrique et non paramétrique se produit lorsque vos données ne répondent pas à une hypothèse du test paramétrique. Cela peut être le cas lorsque vous avez à la fois une petite taille d'échantillon et des données non normales. Cependant, d'autres considérations jouent souvent un rôle car les tests paramétriques peuvent souvent traiter des données non normales. Inversement, les tests non paramétriques ont des hypothèses strictes que vous ne pouvez pas ignorer.
La décision dépend souvent de savoir si la moyenne ou la médiane représente plus précisément le centre de la distribution de vos données.
- Si la moyenne représente avec précision le centre de votre distribution et que la taille de votre échantillon est suffisamment grande, envisagez un test paramétrique car ils sont plus puissants.
- Si la médiane représente mieux le centre de votre distribution, envisagez le test non paramétrique même lorsque vous disposez d'un grand échantillon.
Enfin, si vous disposez d'un échantillon de très petite taille, vous pourriez être bloqué à l'aide d'un test non paramétrique. S'il vous plaît, collectez plus de données la prochaine fois si c'est possible ! Comme vous pouvez le voir, les lignes directrices sur la taille de l'échantillon ne sont pas vraiment si grandes. Vos chances de détecter un effet significatif lorsqu'il existe peuvent être très faibles lorsque vous avez à la fois une petite taille d'échantillon et que vous devez utiliser un test non paramétrique moins efficace !