Parfois, nous devons résoudre des inégalités comme celles-ci :
symbole | Mots | Exemple |
|---|---|---|
| > | plus grand que | x + 3 > 2 |
| < | moins que | 7x < 28 |
| ≥ | Plus grand ou égal à | 5 ≥ x − 1 |
| ≤ | inférieur ou égal à | 2y + 1 ≤ 7 |
Résoudre
Notre objectif est d'avoir x (ou quelle que soit la variable) seul à gauche du signe d'inégalité :
| Quelque chose comme: | x < 5 | |
| ou: | et 11 |
Nous appelons cela "résolu".
Comment résoudre
Résoudre des inégalités, c'est un peu comme résoudre des équations ... nous faisons la plupart des mêmes choses...
... mais il faut aussi faire attention au sens de l'inégalité .
Direction : Dans quel sens la flèche « pointe »
Certaines choses peuvent changer de direction !
< devient >
> devient <
≤ devient ≥
≥ devient ≤
Choses sûres à faire
Ces choses n'affectent pas la direction de l'inégalité:
- Ajouter (ou soustraire) un nombre des deux côtés
- Multiplier (ou diviser) les deux côtés par un nombre positif
- Simplifier un côté
Mais ces choses changent la direction de l'inégalité ("<" devient ">" par exemple):
- Multiplier (ou diviser) les deux côtés par un nombre négatif
- Échanger les côtés gauche et droit
Voici les détails:
Ajouter ou soustraire une valeur
Nous pouvons souvent résoudre des inégalités en ajoutant (ou en soustrayant) un nombre des deux côtés (comme dans Introduction to Algebra ), comme ceci :
Qu'avons-nous fait?
Nous sommes partis de ceci :
Pour ça: | 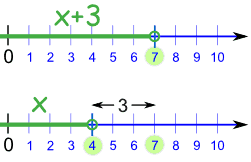 | x+3 < 7
x < 4 | ||
Et cela fonctionne bien pour ajouter et soustraire , car si nous ajoutons (ou soustrayons) le même montant des deux côtés, cela n'affecte pas l'inégalité
Et si je le résolvais, mais que « x » est à droite ?
Peu importe, changez simplement de côté, mais inversez le signe pour qu'il "pointe" toujours la bonne valeur !
Remarque : "x" peut être sur la droite, mais les gens aiment généralement le voir sur le côté gauche.
Multiplier ou diviser par une valeur
Une autre chose que nous faisons est de multiplier ou de diviser les deux côtés par une valeur (comme dans Algèbre - Multiplier ).
Mais nous devons être un peu plus prudents (comme vous le verrez).
Valeurs positives
Tout va bien si on veut multiplier ou diviser par un nombre positif :
Valeurs négatives
| Lorsque nous multiplions ou divisons par un nombre négatif, nous devons inverser l'inégalité. |
Pourquoi?
Eh bien, il suffit de regarder la ligne numérique !
Par exemple, de 3 à 7 est une augmentation ,
mais de -3 à -7 est une diminution.
 | |
| −7 <−3 | 7 > 3 |
Voyez comment le signe d'inégalité s'inverse (de < à >) ?
Essayons un exemple :
(Notez que j'ai inversé l'inégalité sur la même ligne que j'ai divisée par le nombre négatif.)
Alors, n'oubliez pas :
Lorsque vous multipliez ou divisez par un nombre négatif, inversez l'inégalité
Multiplier ou diviser par des variables
Voici un autre exemple (difficile !) :
Pour vous aider à comprendre, imaginez remplacer b par 1 ou −1 dans l'exemple de bx < 3b :
- si b vaut 1 , alors la réponse est x < 3
- mais si b est −1 , alors nous résolvons −x < −3 , et la réponse est x > 3
La réponse pourrait être x < 3 ou x > 3 et nous ne pouvons pas choisir car nous ne connaissons pas b .
Donc:N'essayez pas de diviser par une variable pour résoudre une inégalité (à moins que vous ne sachiez que la variable est toujours positive ou toujours négative).
Un plus grand exemple
Deux inégalités à la fois !
Comment résoudre quelque chose avec deux inégalités à la fois ?
Sommaire
- De nombreuses inégalités simples peuvent être résolues en ajoutant, soustrayant, multipliant ou divisant les deux côtés jusqu'à ce que vous vous retrouviez avec la variable seule.
- Mais ces choses vont changer la direction de l'inégalité:
- Multiplier ou diviser les deux côtés par un nombre négatif
- Échanger les côtés gauche et droit
- Ne multipliez ni ne divisez par une variable (sauf si vous savez qu'elle est toujours positive ou toujours négative)


