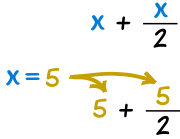Algebra - Substitution

« Remplacer » signifie mettre à la place d'un autre.

Substitution

En algèbre, "Substitution" signifie mettre des nombres où les lettres sont :

	Quand nous avons:	x − 2
	Et on sait que x=6 ...
	... alors on peut "substituer" 6 à x :	6 − 2 = 4

 

Exemple : Quand x=2, qu'est-ce que 10/x + 4 ?

Mettez "2" où "x" est :

10/2 + 4 = 5 + 4 = 9

Exemple : Quand x=5, qu'est-ce que x + x/2 ?

Mettez "5" où "x" est :

5 + 5/2 = 5 + 2.5 = 7.5

Exemple : Si x=3 et y=4, alors qu'est-ce que x ² + xy ?

Mettez "3" où "x" est, et "4" où "y" est :

3² + 3×4 = 3×3 + 12 = 21

Exemple : Si x=3 (mais nous ne savons pas "y"), alors qu'est-ce que x ² + xy ?

Mettez "3" où "x" est :

3 ² + 3 ans = 9 + 3 ans

(c'est aussi loin que nous pouvons obtenir)

Comme l'a montré ce dernier exemple, il se peut que nous n'obtenions pas toujours un nombre pour une réponse, parfois juste une formule plus simple.

Nombres négatifs

Lorsque vous remplacez des nombres négatifs, mettez () autour d'eux pour que les calculs soient corrects.

Exemple : Si x = −2 , alors qu'est-ce que 1 − x + x ² ?

Mettez "(−2)" où "x" est :

1 − (−2) + (−2)² = 1 + 2 + 4 = 7

 

Dans ce dernier exemple :

• le − (−2) est devenu +2
• le (−2) ² est devenu +4

à cause de ces règles spéciales :

	Régner	Ajouter ou soustraire		Multiplier ou diviser
	Deux signes semblables deviennent un signe positif	3+(+2) = 3 + 2 = 5		3 × 2 = 6
		6−(−3) = 6 + 3 = 9		(−3) × (−2) = 6
	Deux signes différents deviennent un signe négatif	7+(−2) = 7 − 2 = 5		3 × (−2) = −6
		8−(+2) = 8 − 2 = 6		(−3) × 2 = −6